La photogrammétrie permet de reconstituer et de mesurer une scène à partir de photographies prises depuis des points de vue différents. Utilisée pour la première fois en 1849 par Aimé Laussedat sur la façade des Invalides, elle a été révolutionnée par les récents progrès de l’informatique.
Parmi les produits de la photogrammétrie, on peut citer les orthophotographies, les modèles 3D texturés et, depuis quelques temps, les nuages de points. Les avantages de la photogrammétrie sont nombreux : une acquisition généralement rapide et du matériel léger permettant de relever des endroits parfois peu accessibles.
Cette technique présente cependant quelques inconvénients notamment une précision finale relativement variable, dépendant de la qualité des prises de vue. De plus, la photogrammétrie ne fonctionne pas directement sur des surfaces non texturées (verre, métal poli…) ; un défaut pouvant être pallié par la projection d’une lumière structurée.
Un appareil photographique ne doit pas être choisi au hasard, plusieurs grandeurs spécifiques sont à prendre en compte avant de réaliser un chantier de mesures.
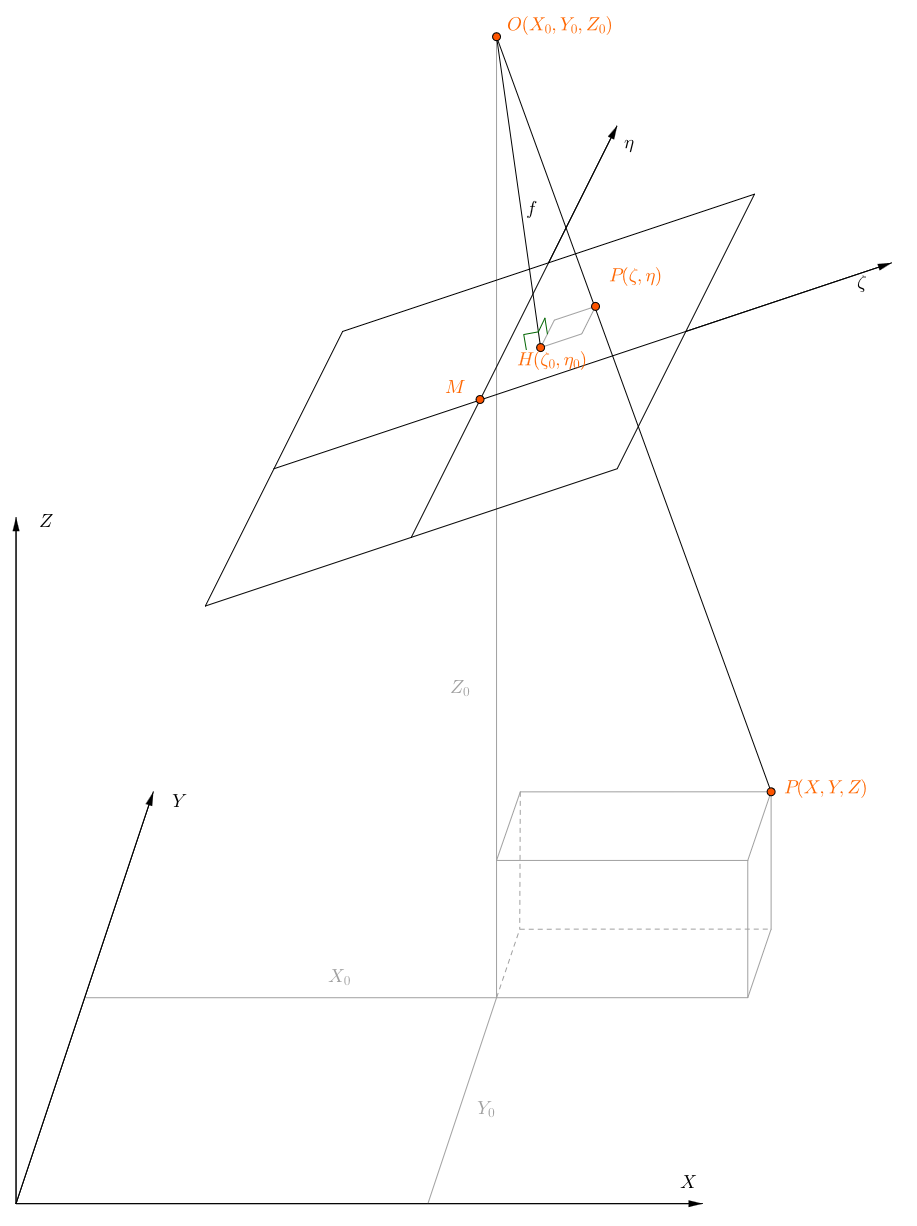
Figure : Schéma fondamental de la photogrammétrie.
O est le centre de perspective de la caméra, f la distance focale.
Le repère général est (X, Y, Z), le repère de la caméra est (ζ, η). (Source : Karl Kraus).
En optique, une distance focale ou distance principale d’une lentille est la distance algébrique entre l’un des plans principaux (image ou objet) et le foyer correspondant. En photographie, le terme distance focale désigne la distance focale image, c’est-à-dire la distance physique entre le centre de perspective et le plan image.
Dans le domaine de l’optique, le terme point principal correspond à l’intersection entre l’axe optique et le plan principal image. Cependant, l’usage veut qu’en photogrammétrie le terme ait un sens différent. En photogrammétrie ce point est appelé centre de perspective et le point principal désignera le point principal de symétrie. Le point principal de symétrie correspond à la projection selon la normale du centre de perspective (correspondant à l’axe optique dans un appareil idéal) sur le plan image (le capteur). Les distorsions radiales et tangentielles sont considérées comme nulles en ce point. Les caméras sont généralement conçues pour que le point principal de symétrie soit au centre de l’image finale, mais des exceptions existent cependant.
La distance focale est le plus souvent notée f ou c.
Le diaphragme est un dispositif mécanique présent dans les appareils photographiques et régulant la quantité de lumière entrant dans l’objectif. Une modification de l’ouverture du diaphragme a également un effet sur la profondeur de champ.
La distance entre l’objectif et le premier plan net, lorsque la mise au point est à l’infini, est nommée la distance hyperfocale H. Soit N le nombre d’ouverture (correspondant à la distance focale divisée par le diamètre de la lentille de l’objectif), D la distance de mise au point et CoC la valeur du cercle de confusion, on peut approximer en photogrammétrie :
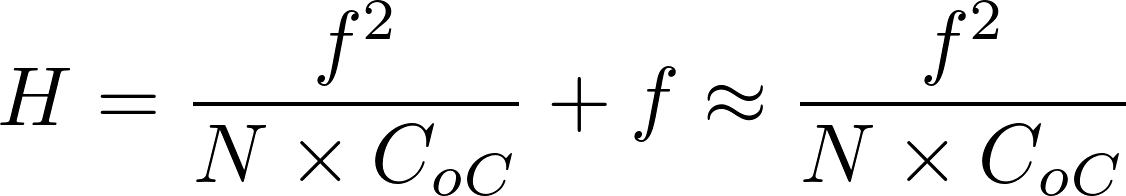


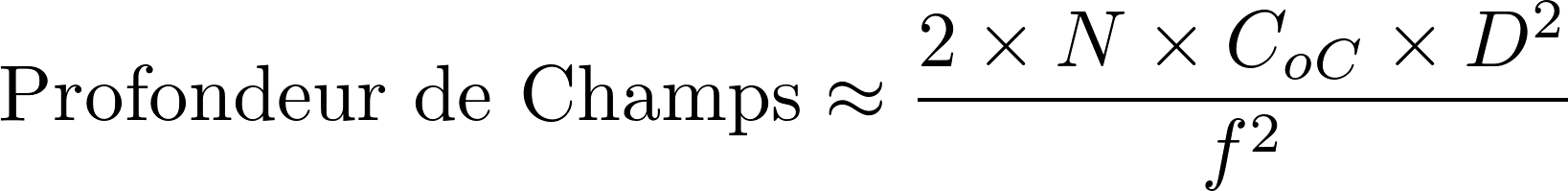
La distance de mise au point est généralement infinie en photogrammétrie architecturale ou aérienne. De plus, les distorsions ont tendance à s’accentuer sur les bords de l’objectif. En photogrammétrie, il est donc d’usage de chercher à avoir le diaphragme le moins ouvert possible afin de limiter ces effets.
La sensibilité d’une pellicule ou d’un capteur photographique à la lumière est également un paramètre important. Elle est généralement mesurée sous la forme d’une sensibilité ISO et tient son nom de l’Institut International de Normalisation (ISO). Plus la pellicule est sensible, moins elle aura besoin d’être exposée à la lumière pour réaliser un cliché.
Cependant en photographie argentique, la contrepartie d’un temps d’exposition faible est l’augmentation de la granularité de l’image et une baisse de la résolution. En photographie numérique, une sensibilité élevée augmente également le bruit sur l’image. Il est donc conseillé d’utiliser des sensibilités de pellicule faibles pour les applications photogrammétriques.
Diaphragme peu ouvert, sensibilité basse… Ces deux éléments tendent à nous faire penser que pour prendre une photo exploitable, le temps d’exposition doit être élevé. Si la photo est prise depuis un appareil placé sur un trépied, ceci est généralement possible. Néanmoins cela n’est pas envisageable dans le cas de la photogrammétrie aérienne. Du fait d’un appareil toujours en mouvement, une exposition trop longue pourrait causer des phénomènes de flous. Il est donc nécessaire de faire un compromis entre ces différents paramètres.
Dans le cadre d’un projet photogrammétrique, il est essentiel de détecter des points homologues entre les différentes images. Autrefois, ils devaient être pointés manuellement par l’utilisateur, mais de nos jours, l’informatique permet d’extraire et de mettre en correspondance des milliers de points par image. L’algorithme SIFT, publié au sein de la communauté travaillant sur la vision par ordinateur en 1999 et développé durant le début des années 2000 (Lowe, D. G., 1999, 2004), est l’une des méthodes les plus courantes.
Il est peu sensible au bruit, aux rotations ou encore aux changements d’échelles, mais réagit mal en cas de changements de points de vue trop importants. Dans le cadre d’un projet photogrammétrique, il est essentiel de détecter des points homologues entre les différentes images.
Il fonctionne en plusieurs étapes :
Au cours de la première étape, une série de filtres gaussiens avec comme paramètre la racine de la variance kiσ est appliquée sous la forme d’une matrice de convolution. La variable ki étant un entier strictement positif.
Soit L le résultat de la convolution, G le filtre gaussien et I l’image traitée.
Cette convolution agit comme un filtre passe-bas, elle a pour effet de lisser l’image et de créer un effet de flou. Ce filtre est appliqué avec une série de valeur de ki. Ce qui permet d’obtenir une série d’images ayant un flou d’intensité croissante.
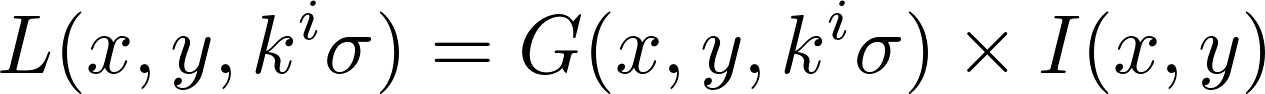
La différence de deux images ayant une valeur de flou différente (différence de gaussienne D) permet de faire ressortir les changement brusque de valeur de pixels, c’est-à-dire les détails et les contours.
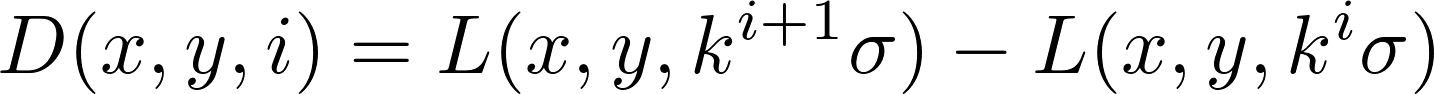
Par exemple sur cette image de notre chantier du lac Noir, nous avons appliqué un filtre gaussien d’écart type σ = 10 pixels. Nous avons ensuite effectué la différence entre l’image floutée et l’image originale (différence de gaussienne à l’ordre 1). Comme on le voit, les arêtes et les points saillants sont mis en évidence :
 |
 |
| Figure : Image et sa différence gaussienne de paramètre 10 pixels. Les valeurs numériques de la différence étant faible (entre 0 et 40), les contrastes ont été rehaussés. | |
Une recherche des extremums, comparant chaque pixel à ses 26 voisins immédiats (voisins géométriques appartenant à la différence de gaussiennes du point, mais également pour les différences précédentes et suivantes), est ensuite effectuée. Un point sera considéré comme un point-clé si et seulement si il a une valeur strictement inférieur ou strictement supérieur à ses 26 voisins.
Un point-clé (x,y,i) est donc défini par sa position, mais aussi par son échelle. L’utilisation d’une pyramide est recommandée afin de réduire le temps de calcul pour les images floutées.
Des coordonnées améliorées pour les points-candidats sont ensuite calculées par interpolation afin d’obtenir des descripteurs avec une résolution plus fine que le pixel, puis les points à faible contraste sont éliminés, tout comme ceux situés sur des arêtes (considérés comme instables). Les points clés de l’image sont ainsi définis.
L’étape suivante consiste à calculer un descripteur pour chaque point ; c’est à partir de ce dernier que sera effectuée la mise en correspondance.
Nous commençons par assigner une orientation θ au point, à partir de la direction des gradients à proximité ; celle-ci est essentielle. En effet le descripteur est calculé en fonction de cette orientation, ce qui rend la méthode invariante aux rotations. À cette étape les points sont alors définis par (x,y,i,θ).
Le descripteur en tant que tel est ensuite calculé : on prend en compte une région de 16 × 16 pixels centrée sur le point clé, subdivisée en zones de 4 × 4.
Différents traitements sont effectués sur les histogrammes de ces 16 zones ; le descripteur final est donc un vecteur de dimension 128.
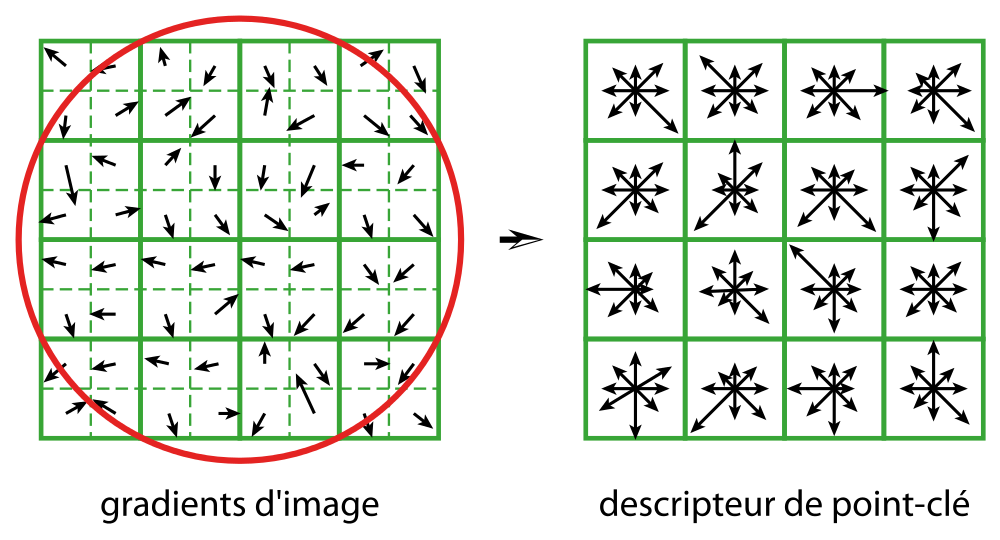 |
| Figure : Descripteur SIFT (Lowe 2004). Pour des raisons de clarté du schéma le gradient d’image est d’une taille de 8 par 8 pixels au lieu des 16 par 16 comme utilisé dans l’algorithme. |
Ces détecteurs sont utilisés pour la mise en correspondance des images. Pour un point donné, l’homologue le plus probable est celui le plus proche par la distance euclidienne. Bien évidemment cette opération ne tenant pas compte de la géométrie des objets, donne lieu à de nombreuses erreurs. Certains points n’ont en effet pas d’homologues dans les autres images.
Si au moins trois points proches sont détectés comme homologues, ceux-ci sont considérés comme probablement plus corrects qu’un point seul. De tels groupes sont utilisés pour vérifier la cohérence du modèle géométrique. De cette manière, la correspondance est validée ou rejetée.
Une fois que les positions des caméras sont connues dans l’espace en coordonnées, on cherche à obtenir un nuage de points dense. Les techniques de corrélation dense vont nous permettre de trouver une solution à ce problème. On cherche à projeter les pixels des différentes photos dans l’espace. Connaissant la position et la calibration de la caméra, la droite sur laquelle se trouve le point est déterminable. Reste maintenant à connaître la profondeur… Pour cela, on s’aide des autres images prises à proximité.
Un coefficient de corrélation est calculé entre les valeurs numériques des images pour un point à chaque endroit de la droite. L’endroit où le coefficient de corrélation est le plus important est également celui où il est le plus probable que le point se trouve.
En répétant cette opération pour tous les pixels des photos et en éliminant ceux pour lesquels le coefficient de corrélation est inférieur à un certain seuil, on obtient un nuage de points densifié.
Notez que pour pouvoir effectuer cette opération de corrélation, il est nécessaire d’avoir du recouvrement entre les photos.